Как работает Big O нотация в JavaScript

Development, Java | Amber | Комментировать запись

В этом мануале мы поговорим о том, что такое Big O нотация и как она работает.

Читайте также: Как работают сервис-воркеры в JavaScript

В некоторых примерах далее мы будем ссылаться на следующие два массива, один из них состоит из 5 элементов, а другой – из 50.

const smArr = [5, 3, 2, 35, 2];

const bigArr = [5, 3, 2, 35, 2, 5, 3, 2, 35, 2, 5, 3, 2, 35, 2, 5, 3, 2, 35, 2, 5, 3, 2, 35, 2, 5, 3, 2, 35, 2, 5, 3, 2, 35, 2, 5, 3, 2, 35, 2, 5, 3, 2, 35, 2, 5, 3, 2, 35, 2];

Также мы будем использовать удобный Performance API для измерения разницы во времени выполнения.

Что такое Big O нотация?

Big O нотация — это просто способ представить общий рост вычислительной сложности задачи по мере увеличения набора данных. Существуют и другие обозначения, однако Big O нотация используется чаще всего, поскольку она фокусируется на сценарии наихудшего случая, который легче оценить и обдумать. Сценарий наихудшего случая – это сценарий, при котором для выполнения задачи требуется наибольшее количество операций.

Когда вы узнаете об алгоритмах больше, вы увидите, что эти выражения часто используются.

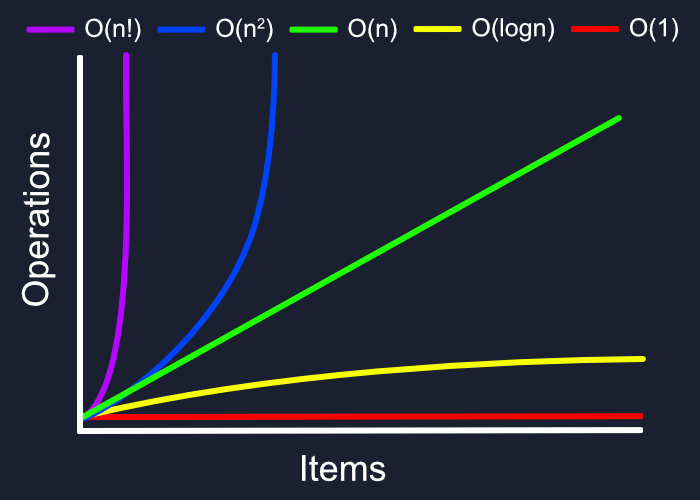
По мере того, как вы будете узнавать больше о Big O нотации, вы, вероятно, увидите много разных вариантов этого графика (среди них будут и лучшие). Мы хотим, чтобы сложность кода была как можно более низкой и прямой, в идеале избегая всего, что превышает O(n).

Алгоритм О(1)

Это идеал, независимо от того, сколько в массиве элементов, будь их один или миллион, количество времени на выполнение останется прежним. Большинство операций, выполняющих одну операцию, работают по алгоритму O(1). Отправка в массив, получение элемента по определенному индексу, добавление дочернего элемента и т. д. займет одинаковое количество времени независимо от длины массива.

const a1 = performance.now();
smArr.push(27);
const a2 = performance.now();
console.log(`Time: ${a2 - a1}`); // Less than 1 Millisecond


const b1 = performance.now();
bigArr.push(27);
const b2 = performance.now();
console.log(`Time: ${b2 - b1}`); // Less than 1 Millisecond

Алгоритм O(n)

По умолчанию все циклы относятся к операциям линейного роста, поскольку между размером данных и временем выполнения существует взаимосвязь один к одному. Таким образом, массив с в 1000 раз большим количеством элементов займет ровно в 1000 раз больше времени.

const a1 = performance.now();
smArr.forEach(item => console.log(item));
const a2 = performance.now();
console.log(`Time: ${a2 - a1}`); // 3 Milliseconds

const b1 = performance.now();
bigArr.forEach(item => console.log(item));
const b2 = performance.now();
console.log(`Time: ${b2 - b1}`); // 13 Milliseconds

Алгоритм O(n^2)

Экспоненциальный рост — это ловушка, в которую мы все попадаем хотя бы раз. Нужно найти подходящую пару для каждого элемента в массиве? Вложение цикла внутрь другого цикла — отличный способ превратить массив из 1000 элементов в миллион операций поиска, которые заморозят ваш браузер. Всегда лучше выполнять 2000 операций в двух отдельных циклах, чем миллион в двух вложенных циклах.

const a1 = performance.now();
smArr.forEach(() => {
    arr2.forEach(item => console.log(item));
});
const a2 = performance.now();
console.log(`Time: ${a2 - a1}`); // 8 Milliseconds


const b1 = performance.now();
bigArr.forEach(() => {
    arr2.forEach(item => console.log(item));
});
const b2 = performance.now();
console.log(`Time: ${b2 - b1}`); // 307 Milliseconds

Алгоритм O(log n)

Это алгоритм логарифмического роста. Пожалуй, лучшая аналогия, которую можно придумать для объяснения этого алгоритма — это представить себе поиск слова «нотация» в словаре. Вы не станете пересматривать все записи одну за другой, вместо этого вы найдете раздел «N», затем, возможно, страницу «OPQ», затем выполните поиск по списку в алфавитном порядке, пока не найдете искомое слово.

При таком подходе количество времени, необходимое для поиска слова, по-прежнему будет зависеть от размера словаря, но не со скоростью O(n). Поскольку этот алгоритм выполняет поиск в конкретных разделах, не просматривая большую часть данных, поиск по тысяче элементов может занять менее 10 операций, а по миллиону — менее 20, что даст вам максимальную отдачу.

В этом примере мы попробуем выполнить простую быструю сортировку.

const sort = arr => {
  if (arr.length < 2) return arr;

  let pivot = arr[0];
  let left = [];
  let right = [];

  for (let i = 1, total = arr.length; i < total; i++) {
    if (arr[i] < pivot) left.push(arr[i]);
    else right.push(arr[i]);
  };
  return [
    ...sort(left),
    pivot,
    ...sort(right)
  ];
};

sort(smArr); // 0 Milliseconds
sort(bigArr); // 1 Millisecond

Алгоритм O(n!)

Наконец, одна из худших возможностей — факторный рост. Классическим примером этого алгоритма является задача о коммивояжере. Допустим, у нас есть несколько городов в разной удаленности. Как найти кратчайший маршрут, соединяющий их все и возвращающийся в исходную точку? Самый топорный метод: посчитать все возможные маршруты между городами, – это станет факториалом и быстро выйдет из-под контроля.

Поскольку эта задача очень быстро усложняется, мы продемонстрируем эту сложность на короткой рекурсивной функции. Эта функция умножает число на собственную функцию, принимающую себя минус единицу. Каждая цифра в нашем факториале будет выполнять свою собственную функцию, пока не достигнет 0, при этом каждый рекурсивный слой будет добавлять свой результат к нашему исходному числу. Таким образом, 3 умножается на 2, что запускает функцию, умножаемую на 1, которая запускает ее снова, чтобы остановиться на 0, возвращая 6. Рекурсия довольно легко превращается в путаницу.

Примечание: Факториал — это просто произведение всех чисел, идущих до этого числа включительно. То есть, 6! – это 1x2x3x4x5x6 = 720.

const factorial = n => {
  let num = n;

  if (n === 0) return 1
  for (let i = 0; i < n; i++) {
    num = n * factorial(n - 1);
  };

  return num;
};

factorial(1); // 2 Milliseconds
factorial(5); // 3 Milliseconds
factorial(10); // 85 Milliseconds
factorial(12); //  11,942 Milliseconds

Мы хотели показать пример с factorial(15), однако после 12 все становилось слишком сложно, что приводило к сбою страницы – и это лучшее доказательство, что этого следует избегать.

Заключение

Поддержка кода в его максимально возможной производительности может показаться очевидным решением вопроса; однако, скорее всего, почти каждый разработчик хотя бы раз создавал двойные или даже тройные вложенные циклы, просто потому что «это работает». Big O нотация позволяет нам думать о сложности и выражать ее так, как мы никогда раньше не могли.